Cum de a construi un număr de pătrat

În general, gradul este scris ca ^ n. Această intrare indică faptul că un număr este înmulțit cu el însuși de n ori.
Expresia a ^ n este gradul de u,
a - un număr care nivelul de bază,






n - este numărul, exponent. De exemplu, a = 4, n = 5,
Apoi vom scrie 4 ^ 5 = 4 * 4 * 4 * 4 * 4 = 1024

Gradul de n poate fi negativ
n = -1, -2, -3, etc.
Pentru a calcula gradul de numere negative, acesta trebuie să fie coborât la numitor.
a ^ (- n) = (1 / a) ^ n = 1 / a * 1 / a * 1 / a * ... * 1 / a = 1 / (a ​​^ n)
Luați în considerare exemplul
2 ^ (- 3) = (1/2) ^ 3 = 1/2 * 1/2 * 1/2 = 1 / (2 ^ 3) = 1/8 = 0.125

După cum se poate observa din exemplul -3 grade de 2 poate fi calculată în moduri diferite.
1) se calculează întâi fracția 1/2 = 0,5; și apoi a ridicat la puterea 3
și anume ^ 3 = 0,5 0,5 * 0,5 * 0,5 = 0,125
2) construi întâi numitorul la puterea 3 = 2 ^ 2 * 2 * 2 = 8, iar apoi se calculează fracția 1/8 = 0,125.

Acum, se calculează gradul de -1 pentru numărul, adică n = -1. Regulile discutate mai sus sunt potrivite pentru acest caz.
a ^ (- 1) = (1 / a) ^ 1 = 1 / (a ​​^ 1) = 1 / a
De exemplu, numărul 5 erecta în grad -1
5 ^ (- 1) = (1/5) ^ 1 = 1 / (5 ^ 1) = 1/5 = 0,2.

De exemplu, arată în mod clar că un număr de grad -1 - o fracțiune de numere inverse.
5 reprezintă numărul de fracțiuni 5/1, apoi 5 ^ (- 1) nu pot fi considerate aritmetic, și scrie imediat fracție inversă 5/1 este 1 / 5.Tak, 15 ^ (- 1) = 1/15,
6 ^ (- 1) = 1/6,
25 ^ (- 1) = 1/25

Odată cu construcția unei puteri negative trebuie amintit faptul că numărul nu poate fi zero. Conform regulii, noi trebuie să reducă numărul de la numitor. Un zero nu poate fi la numitor, pentru că nu se poate diviza de la zero.

Uneori, atunci când se lucrează cu puteri pentru a simplifica calculul fracționată în mod specific înlocuit în toată amploarea -1
1/6 = 6 ^ (- 1)
1/52 = 52 ^ (- 1).

În rezolvarea problemelor aritmetice si algebrice este uneori necesară pentru a construi o fracție în pătrat. Cel mai simplu mod de a face acest lucru atunci când o fracție zecimală - doar un calculator obișnuit. Cu toate acestea, în cazul în care fracțiunea obișnuită sau mixtă, unele dificultăți pot apărea în timpul construcției acestor numere într-un pătrat.

• Calculator, calculator, aplicații Excel.

Pentru a construi o fracție zecimală în pătrat. Ia un calculator științific, introduceți-l ridicat în kvadratdrob și apăsați construcția celui de al doilea grad. Acest buton este pe cele mai multe calculatoare desemnate ca „h²“. În standard, funcția de calculator pentru Windows cvadratura se pare ca «x ^ 2" . De exemplu, pătratul zecimal este egal cu 3.14: 3,14² = 9,8596.

Pentru a pătrat zecimal pe un (contabilitate) Calculator normale, înmulțiți acest număr de la sine. Apropo, în unele modele de calculatoare cu condiția posibilitatea unui număr ridicat la pătrat, chiar și în absența unui buton dedicat. Prin urmare, pre-citit instrucțiuni la calculator special. Uneori, exemple de exponentiere „viclenie“, se arată în capacul din spate sau pe cutia calculatorului. De exemplu, pe mai multe calculatoare pentru construirea de pătrat, trebuie doar să apăsați butonul „x“ și „=“.

Pentru cvadratura fracțiune comună (constând din numărătorul și numitorul), ridicat la pătrat individual numărătorul și numitorul fracției. Aceasta este, utilizați următoarea regulă: (c / o) ² = ch² / z² unde h - numărătorului, s - numitor drobi.Primer: (3/4) ² = 3² / 4² = 9/16.

Dacă sunt construite în interiorul kvadratdrob - mixt (compus dintr-o parte întreagă și o fracție comună), pre-l aduce la mintea obișnuită. Aceasta este, se aplică următoarea formulă: (n c / o) ² = ((n * h + h) / h) ² = (s + n * h) ² / z² unde n - partea întreagă a drobi.Primer mixt: (3 2/5) ² = ((5 * 3 + 2) / 5) ² = (3 * 5 + 2) ² / 5² = 17² / 5² = 289/25 = 11 14/25.

evidențiați pătrat metodei binom este utilizată pentru simplificarea expresiilor greoaie, precum și pentru a rezolva ecuații pătratice. În practică, este de obicei combinată cu alte tehnici, inclusiv factoring, grupare, și așa mai departe.

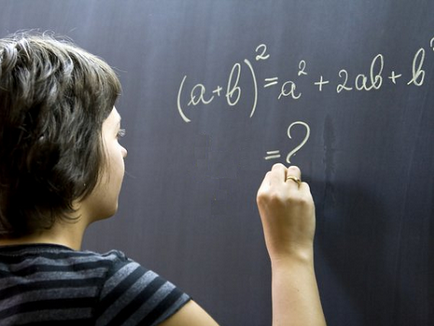
Metoda de izolare a unui binom plin pătrat bazat pe utilizarea a două formule Acronim multiplicării polinom. Aceste formule sunt cazuri speciale ale teoremei binom pentru gradul doi și pentru a simplifica expresia necesară, astfel încât a fost posibil să se efectueze declin sau factoring ulterioare:






(+ N M) ² = mp + 2 · m · n + n²;
(M - n) ² = m² - 2 · m · n + n².

Conform acestei metode de polinomul original este necesară pentru a selecta cele două pătrate și suma monoamele / diferență de produsul lor dublu. Această metodă are sens, în cazul în care cele mai mari termeni de putere cu cel puțin 2. Să presupunem că, având în vedere sarcina la factorul jos, gradul de următoarea expresie:
4 · y ^ 4 + z ^ 4

Pentru a rezolva problema, trebuie să folosim metoda de alocare a unui pătrat perfect. Astfel, expresia este format din două monoamele cu variabile chiar grad. Prin urmare, se poate identifica fiecare dintre ele prin m și n:
m = 2 · Ya; n = z².

Acum trebuie să aducem expresia originală la forma (m + n) ². Acesta este prezent deja pătratelor acestor termeni, dar nu suficient de produs dublu. Trebuie să o adăugați în mod artificial, și apoi scade:
(2 · Ya) ² + 2 · 2 · · z² + Ya (z²) ² - 2 · 2 · · z² = Ya (2 · + z² Ya) ² - 4 · · z² Ya.

În expresia rezultată se poate vedea diferența dintre pătrate cu formula:
(2 · + z² Ya) ² - (2 · y · z) ² = (2 · + z² Ya - 2 · y · z) · (2 ​​· + z² + Ya 2 · y · z).

Astfel, metoda constă în două etape: separarea unui monoamele plin pătrat m și n, adăugarea și scăderea produsului dublu. Metoda de izolare a unei binom pătrat perfect poate fi folosit nu numai singur, ci și în combinație cu alte metode: emiterea parantezelor comune multiple, substituție variabilă, termeni și alte grupuri.

Exemplul 2.
Evidențiați pătrat plin în expresia:
4 + 2 · · Ya y · z + z².
Decizie.
4 · Ya + 2 · y · z + z² = [m = 2 · y n = z] = (2 · y) ² + 2 · 2 · y · z + (z) ² - 2 · y · z = (2 · y + z) ² - 2 · y · z.

Metoda este utilizată pentru găsirea rădăcinilor unei ecuații pătratice. Partea stângă a ecuației este o formă trinomial a · + b · Ya y + c, unde a, c b și - niște numere cu ≠ 0.
o · Ya + b · y + c = a · (Ya + (b / a) · y) + c = a · (Ya + 2 · (b / (2 · a)) · y) + c = a · (Ya + 2 · (b / (2 · a)) · y + b² / (4 · a²)) + c - b² / (4 · a) = a · (y + b / (2 · a)) ² - (b² - 4 · a · c) / (4 · a).

Aceste calcule conduc la conceptul unui discriminantă care este egal cu (b² - 4 · a · c) / (4 · a), iar rădăcinile ecuației egală cu:
y_1,2 = ± (b / (2 • a)) ± √ ((b² - 4 · a · c) / (4 · a)).

Operațiunea exponentiere este „binar“, adică are doi parametri de intrare necesare și o ieșire. Unul dintre parametrii inițiali se numește un exponent și determină numărul de ori că operațiunea de multiplicare trebuie aplicat al doilea parametru - bază. Baza poate fi pozitivă sau negativă.

Utilizați în construcția de puterea unui număr negativ, normele obișnuite de funcționare. În ceea ce privește numerele pozitive, exponentiala înseamnă înmulțirea valorii inițiale pentru sine numărul de ori mai puțin decât un exponent. De exemplu, pentru a crește numărul de a patra putere -2, este necesar să se multiplice trei: -2⁴ = -2 * (- 2) * (- 2) * (- 2) = 16.

Înmulțirea a două numere negative dă întotdeauna o valoare pozitivă, iar rezultatul acestei operații pentru variabile cu diferite semne va fi un număr negativ. De aici putem trage concluzia că, odată cu construcția valorilor negative indicelui chiar de gradul obținut trebuie întotdeauna un număr pozitiv, iar pentru indicii impare rezultat va fi întotdeauna mai mică decât zero. Utilizați această proprietate pentru a verifica calculele efectuate. De exemplu, a cincea putere -2 ar trebui să fie un număr negativ -2⁵ = -2 * (- 2) * (- 2) * (- 2) * (- 2) = - 32, iar al șaselea -2 - pozitiv -2⁶ = -2 * (- 2) * (- 2) * (- 2) * (- 2) * (- 2) = 64.

Atunci când ridicarea unui număr negativ în index grad pot fi aduse în format comun fracțiune - de exemplu, -64 grade la ⅔. Această cifră indică faptul că valoarea inițială trebuie ridicată la o putere egală cu numărătorul fracției și se extrage din ea rădăcina grad egal numitor. O parte din această operațiune este luată în considerare în etapele anterioare, dar aici ar trebui să acorde o atenție la alta.

Extract de rădăcină - o funcție ciudat, adică numere reale negativ, acesta poate fi utilizat numai pentru exponent ciudat. Pentru această funcție chiar nu contează. Prin urmare, în cazul în care condițiile de sarcini necesare pentru a construi un număr negativ, la o putere fracționată, cu un numitor chiar, atunci problema nu are nici o soluție. In alte cazuri, efectuați prima operație a primelor două etape, folosind ca exponent al numărătorului, și apoi îndepărtați rădăcina la gradul de numitor.

Puterea formatului de înregistrare - este o formă prescurtată a bazei de multiplicare operație de scriere de la sine. Cu numărul reprezentat într-o formă care poate fi efectuat aceleași operații ca și cu orice alte numere, inclusiv erecta în grad. De exemplu, este posibil să se construiască într-un număr arbitrar și stepenkvadrat rezultat-dezvoltarea artei nu va fi nici o dificultate.

• Accesul la Internet sau un calculator pentru Windows.

Pentru construirea de pătrat și în gradul de utilizare a numerelor generale regula exponentiala care are deja un indicator de putere. Când astfel de parametri de funcționare sunt multiplicate, iar baza este aceeași. Dacă substratul este notat ca x, iar exponenții inițiale și suplimentare - atât a cât și b, este de obicei scrisă într-o formă generală, puteți: (xᵃ) ᵇ = xᵃᵇ.

Pentru calcule practice, cel mai simplu mod de a utiliza motorul de căutare Google - acesta este construit este foarte ușor de utilizat calculator. De exemplu, dacă doriți să ridice numărul 6 în a cincea stepenkvadrat, du-te la principalul motor pagina de căutare și tipul în cererea corespunzătoare. Formulați aceasta, puteți: (6 ^ 2) ^ 5 - ^ reprezintă aici pictograma grade. O poate calcula independent exponent rezultat conform formulei din etapa anterioară și de a formula interogarea: 6 ~ 10. Sau încredere pentru a face acest lucru Google, este suficient să introduceți această interogare: 6 ^ (2 * 5). Pentru fiecare dintre aceste exemple de realizare, motorul de căutare va returna același calculator răspuns: 60466176.

Apăsați Alt + 2 la interfața aplicației este un nou buton cu ridicarea unei funcții într-o măsură arbitrară. Apoi, introduceți baza - în exemplul al doilea pas este numărul de 6 - și primul x² faceți clic pe butonul, apoi butonul x. Introduceți exponentul la care doriți să construiască un pătrat - să utilizeze un exemplu care numărul 5. Apăsați butonul Enter și calculatorul va arăta rezultatul final al operațiunii.