Cum de a găsi perimetrul triunghiului

pași Editare

Metoda 1 de la 3:
Pe trei laturi ale datelor din dreapta

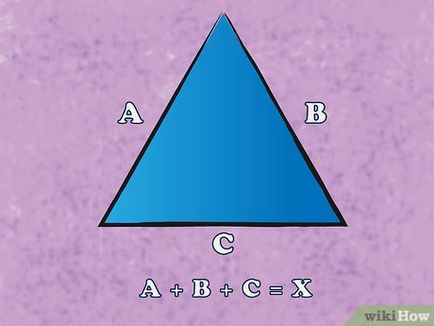
Pentru a găsi perimetrul folosind formula: P = a + b + c, unde a, b, c - lungimea celor trei părți, P - perimetru.

Găsiți lungimile toate cele trei laturi. In acest exemplu: a = 5, b = 5, c = 5.

• Acesta este un triunghi echilateral, pentru că toate cele trei laturi au aceeași lungime. Dar formula de mai sus se aplică în orice triunghi.

Ori lungimea de toate cele trei laturi pentru a găsi perimetrul. In exemplul nostru: 5 + 5 + 5 = 15, adică P = 15.

• Un alt exemplu: a = 4, b = 3, c = 5. R = 3 + 4 + 5 = 12.

Ca răspuns, nu uitați să specificați unitatea de măsură. În exemplul nostru, partea măsurată în centimetri, astfel încât răspunsul final ar trebui să includă, de asemenea, un centimetru (sau unitate specificată în problema).

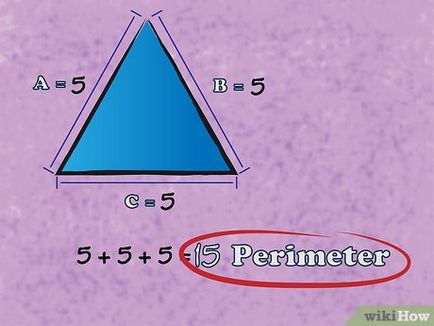
• In acest exemplu, fiecare parte este de 5 cm, astfel încât răspunsul final este: P = 15 cm.

Metoda 2 din 3:
Conform datelor din cele două laturi ale unui triunghi dreptunghic Editare

Amintiți-vă de teorema lui Pitagora. Aceasta teorema descrie relația dintre laturile rectangulare ale triunghiului și este una dintre cele mai cunoscute și utilizate teoremele matematice. [2] Teorema afirmă că orice laturile înclinate triunghi sunt conectate prin următoarea relație: a 2 + b 2 = c 2. în cazul în care a, b - picioare, cu - ipotenuza. [3]

Egal triunghi și marchează ambele părți a, b, c. Cea mai lungă parte a unui triunghi dreptunghic - este ipotenuzei. Acesta se află vizavi de unghi drept. Etichetă ipotenuzei ca „c“. Picioarele (pe părțile laterale adiacente unghiul drept) desemnează atât «a» și «b».

Substitut valorile cunoscute ale părților din teorema lui Pitagora (a 2 + b 2 = c 2). În loc de litere, substitui numărul dat în problema.

• De exemplu, a = 3 și b = 4. suplean aceste valori în teorema lui Pitagora: 3 2 + 4 2 = c 2.
• Un alt exemplu: a = 6 și c = 10. Apoi: 2 6 + b 2 2 = 10

Rezolva ecuația rezultată pentru a găsi o direcție necunoscută. Pentru a face acest lucru, în primul rând pătrat cunoscut lungimea laturilor (pur și simplu, înmulțiți acest număr de la sine). Dacă sunteți în căutarea ipotenuzei, se adaugă pătratele ale celor două părți și din extractul rezultat rădăcina pătrată a sumei. Dacă sunteți în căutarea pentru un picior, scade pătratul celebrului picior pătratului ipotenuzei, și de pulsiunea privat obținut rădăcina pătrată.

• În primul exemplu 3 2 + 4 2 = c 2; 9 + 16 = c 2; 25 = c2; √25 = s. Astfel, c = 25.
• In al doilea exemplu 6 2 2 + b 2 = 10; 36 + b 2 = 100. Transferul 36 în partea dreaptă a ecuației pentru a obține: b 2 = 64; b = √64. Astfel, b = 8.

Ori lungimea celor trei laturi pentru a găsi perimetrul. Să ne amintim că perimetrul este calculat prin formula: P = a + b + c.

• In primul nostru exemplu: P = 3 + 4 + 5 = 12.
• In acest al doilea exemplu: P = 8 + 6 + 10 = 24.

Metoda 3 din 3:
Conform datelor din cele două părți și unghiul dintre ele Edit

Orice parte a unui triunghi poate fi găsit de teorema cosinus, în cazul în care vi se oferă două părți și unghiul dintre ele. Această teoremă este valabilă pentru orice triunghi și este formulă foarte util. Cosinus teorema: c 2 = a 2 + b 2 - 2abcos (C), în care a, b, c - partea a triunghiului, A, B, C - colțuri, laturile respective opuse ale triunghiului. [4] [5]

Egal triunghi și marchează ambele părți a, b, c; desemnează părțile opuse respective ale ambelor unghiuri A, B, C (adică unghiul opus latura „a“ eticheta „A“ și așa mai departe).

• De exemplu, având în vedere un triunghi cu laturile 10 și 12, iar unghiul dintre ele de 97 °, adică a = 10, b = 12, C = 97 °.

Pune datele în formula și de a găsi o latură necunoscută a „c“. În primul rând, la pătrat cunoscute laturi de lungime și ori valorile obținute. Apoi găsește cosinusul unghiului C (folosind un calculator sau calculator on-line). [6] Înmulțire cunoscute lungimile laterale de cosinusul unghiului și la 2 (2abcos (C)). Scădeți valoarea rezultată a sumei pătratelor celor două părți (a 2 + b 2), și veți obține un c 2. Din această cantitate se extrage rădăcina pătrată pentru a localiza lungimea laturii necunoscute „c“. În exemplul nostru:

• c = 10 2 2 + 12 2 - 2 x 10 x 12 x cos (97)
• c 2 = 100 + 144 - (240 x -0,12187)
• c 2 = 244 - (-29.25)
• c 2 = 244 + 29,25
• c 2 = 273.25
• c = 16,53

Ori lungimea celor trei laturi pentru a găsi perimetrul. Să ne amintim că perimetrul este calculat prin formula: P = a + b + c.

• În exemplul nostru P = + 12 + 10 = 16.53 38.53.