Reguli generale pentru întocmirea problemelor duale
Regula 1: Toate restricțiile problemei inițiale membrii liberi trebuie să fie pe partea dreaptă, și membrii cu necunoscut - pe partea stângă.
Regula 2. Problema inițială constrângeri inegalitățile în materie trebuie să fie scrise, astfel încât semnele de inegalitate au fost în aceeași direcție.
Regula 3. În cazul în care semnele de inegalitate în constrângerile ale problemei inițiale "


Regula 4. Fiecare restricție problemă sursă necunoscută corespunde cu problema duală, necunoscut restricție inegalitatea corespunzătoare trebuie să îndeplinească condițiile de non-negativitate și constrângeri de egalitate corespunzătoare necunoscute pot fi de nici un semn.
Regula 5. Funcția obiectiv a problemei dublă are forma
,
unde

Articolul 6. Funcția obiectiv
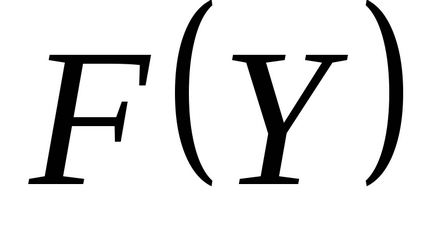

Regula 7. Fiecare neizvestnomuhj, j = 1, 2, ..., n problema inițială corespunde limitei problemei duale. Setul de constrângeri etihn (împreună cu non-negativitate condiții neizvestnyhyi. Constrângerile Inegalitatile relevante ale problemei inițiale) formează un sistem de limitare dublă problemă. Toate constrângerile de problema duală au forma de inegalități, membri liberi care sunt pe laturile din dreapta, și cu membrii neizvestnymiy1, y2. ...,

Toate semnele inegalitatea sunt de forma "


6.2. Soluție simultană a problemelor primare și duale
Soluție simultană a problemelor primare și duale se bazează pe teoria dualității. Teoremele dualitatii ne permit să se stabilească o relație între soluția optimă a unei perechi de probleme duale. Decizia de una dintr-o pereche de probleme duale, sau puteți găsi o soluție optimă la o altă problemă, nu o rezolvare, sau pentru a seta absența acestuia. În următoarele cazuri:
- ambele probleme ale perechilor duale sunt soluții optime;
- una dintre probleme este nici o soluție în vedere funcția obiectiv este nemarginit, iar celălalt are nici o soluție, având în vedere incompatibilitatea sistemului de constrângeri.
Teorema 6.2.1 (prima dualitate teorema). În cazul în care unul dintre obiectivele perechii dual, a solvabili și alte obiecte reciproc solubile, în acest caz, valorile optime ale funcțiilor obiective sunt aceleași. În cazul în care funcția obiectiv este unul dintre obiectivele nu se limitează la (sus - pentru a maximiza problema din partea de jos - pentru a minimiza problema), setul de planuri fezabile pentru alte sarcini este gol.
Această teoremă presupune următoarele
Corolar. Pentru a soluțiilor fezabile


dublă pereche de probleme au fost optime, este necesar și suficient ca funcția obiectiv cu privire la aceste planuri coincid:.
Teorema 6.2.2 (a 2-dualitate teorema). Să fie o pereche simetrică de probleme duale
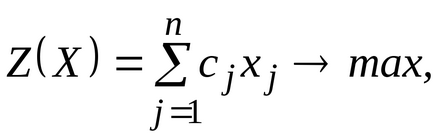


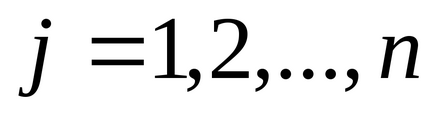


Pentru a soluțiilor fezabile, este perechea optimă soluție de probleme duale, este necesar și suficient ca ecuațiile următoare:
Altfel, dacă înlocuirea soluției optime din numărul i restricțiile care limitează sarcina inițială este realizată ca o inegalitate stricta, TOI coordonata solutiei optime a problemei duale este zero, și invers, eslii coordonata solutiei optime a problemei duale este diferit de zero, toi- adică limitând problema inițială soluția optimă este îndeplinită ca o egalitate.
Exemplul 6.2. Pentru această problemă pentru a face o dublă rezolva metoda grafică și utilizând a doua teorema de dualitate, pentru a găsi o soluție a problemei inițiale:

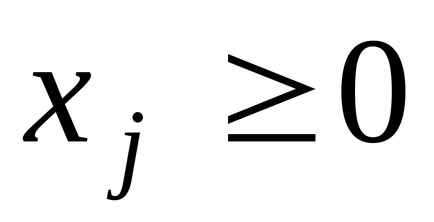

Decizie. Am construit problema dublă

Noi rezolva această problemă prin metoda grafică. Fig. 6 prezintă gama de soluții admisibile ale problemei, normal







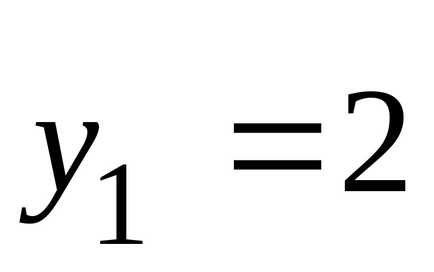

.
Substitut soluția optimă


Conform celei de a doua teorema de dualitate a coordonatelor soluției duale corespunzătoare optimă, adică, problema inițială sunt zero:


