Spring pendul 2

pendul de primăvară este o masă punct material

, atașat la un arc elastic complet fără greutate cu rigiditate . Există două dintre cel mai simplu caz: orizontal (figura 15, A) și verticală (figura 15, b) un pendul.

a) Pendulul orizontal (fig. 15a). Schimbarea de marfă

din poziția de echilibru valoarea funcționează într-o forță elastică napravleniivozvraschayuschaya orizontală(Legea lui Hooke).

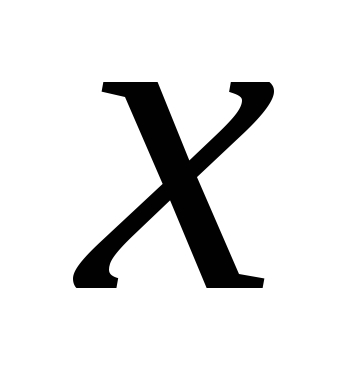
Se presupune că suportul orizontal, pe care slide-uri de încărcare

când vibrațiile sale complet netedă (fără frecare).

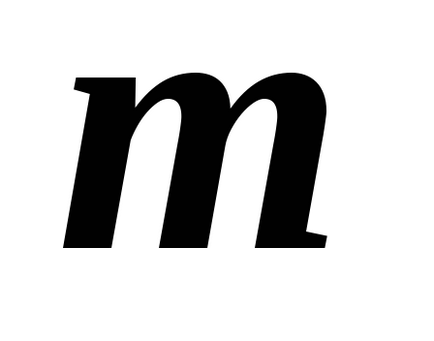
b) Pendulul vertical (figura 15, B). Poziția de echilibru în acest caz, se caracterizează prin condiția:

unde

- mărimea forței elastice care acționează asupra sarcinii la tensiune statică pe arc sub forța gravitațională a sarcinii.

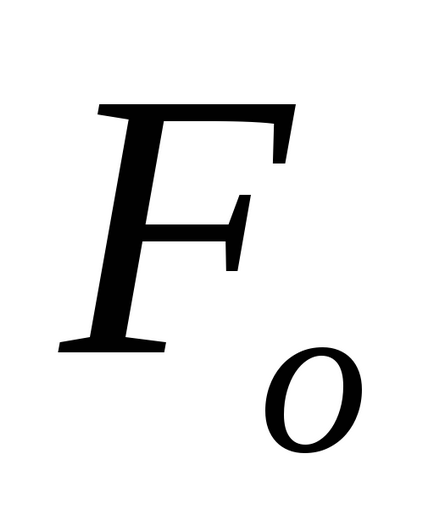
Figura 15. pendul de primăvară: a - b și orizontală - verticală

Dacă întinde un arc și eliberați sarcina, acesta va începe să se ridice. Dacă deplasarea la un anumit punct în timp, va fi

, forța elastică este acum scris ca.

În ambele cazuri, pendulul de primăvară oscilează cu o perioadă

și frecvența ciclică

Pe exemplul examinării pendulului de primăvară, putem concluziona că oscilații armonice - o mișcare cauzată de o forță proporțională cu deplasarea în creștere

. Astfel, în cazul în care forța de revenire a legii lui Hooke seamănă(Ea a primit forțe nazvaniekvaziuprugoy), atunci sistemul trebuie să efectueze vibratii armonice. La momentul trecerii unei poziții de echilibru pe corp nu este acționează forța de revenire, cu toate acestea, corpul de inerție este depășită poziția de echilibru și restaurarea inversează forță.

pendulă

Figura 16. pendulă

Pendulul reprezintă un sistem idealizată sub forma unei particule suspendate într-o lungime fără greutate fir inextensibil

, care suferă oscilații mici, sub gravitate (Fig. 16).

Variante ale pendulului pentru unghiuri mici de deflecție

(Nu mai mare de 5 °) pot fi considerate armonice, și o frecvență ciclică a unui pendul matematic:

2.3. energia corpului la vibratii armonice

Energia transmisă la sistemul vibreaza la o zdruncinătură inițială va transforma periodic energia potențială a arcului va fi deformat să se miște în energie cinetică a încărcăturii în mișcare și înapoi.

Să pendulului primăvară pendulează cu o fază inițială

, și anume(Fig.17).

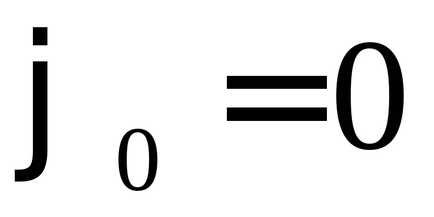
Figura 17. Legea conservării energiei mecanice

oscilațiilor unui pendul de primăvară

La deviația maximă a sarcinii din poziția de echilibru a energiei mecanice totale pendul (energia unui arc deformat cu rigiditate

) este . Când se trece în poziția de echilibru () Energia potențială a arcului devine zero, iar energia mecanică totală a sistemului vibrator este definit ca .

Figura 18 sunt grafice ale dependențelor cinetice, potențialul și energia totală când oscilații armonice sunt descrise funcție sinus trigonometrică (linia punctată) sau cosinus (linie solidă).

Figura 18. Graficele de dependența de timp a cinetic

și energie potențială la vibrații armonice

Graficele (Fig.18) că frecvența de variație a energiei cinetice și de potențial este de două ori frecvența naturală a oscilațiilor armonice.